Phép đơn cấu
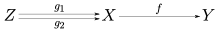
Trong phạm vi của đại số trừu tượng hay đại số phổ dụng, một đơn cấu là một đồng cấu mang tính đơn ánh. Một đơn cấu từ X đến Y thường được ký hiệu bằng ký hiệu .
Trong cơ sở tổng quát hơn của lý thuyết phạm trù, một đơn xạ (còn được gọi là cấu xạ monic) là một cấu xạ có tính khử trái được. Nghĩa là, một mũi tên f : X → Y sao cho với mọi vật Z và mọi cấu xạ g1, g2: Z → X,
Các phép đơn cấu là một sự tổng quát hóa có tính phân loại của các đơn ánh (hay còn được gọi là các hàm "một đối một").
Liên quan đến tính nghịch đảo
[sửa | sửa mã nguồn]Các cấu xạ khả nghịch trái được yêu cầu là phải là đơn cấu: nếu l là phép nghịch đảo trái đối với f (nghĩa là l là phép cấu xạ và ), thì f là monic, bởi
Ví dụ
[sửa | sửa mã nguồn]Mọi phép cấu xạ trong một phạm trù cụ thể mà hàm của nó có tính đơn ánh được gọi là một phép đơn cấu; nói cách khác, nếu các phép đơn cấu là các hàm giữa các tập hợp, thì bất kỳ phép cấu xạ nào là hàm có tính đơn ánh nhất thiết sẽ là một phép đơn cấu theo ý nghĩa phạm trù.
Tham khảo
[sửa | sửa mã nguồn]- Bergman, George (2015). An Invitation to General Algebra and Universal Constructions. Springer. ISBN 978-3-319-11478-1.
- Borceux, Francis (1994). Handbook of Categorical Algebra. Volume 1: Basic Category Theory. Cambridge University Press. ISBN 978-0521061193.
- Hazewinkel, Michiel biên tập (2001), “Monomorphism”, Bách khoa toàn thư Toán học, Springer, ISBN 978-1-55608-010-4
- Van Oosten, Jaap (1995). “Basic Category Theory” (PDF). Brics Lecture Series. BRICS, Computer Science Department, University of Aarhus. ISSN 1395-2048.
- Tsalenko, M.S.; Shulgeifer, E.G. (1974). Foundations of category theory. Nauka. ISBN 5-02-014427-4.




